APPLICATIONS LINEAIRES
Soit f une application de E dans F f :
v ➜V = f(v)
f est
dite « linéaire » si
● pour tout
couple de vecteurs v1 et v2 de E on a f(v1 + v2)
= f(v1) + f(v2)
● pour
tout vecteur v de E et tout réel k on a f(kv) = kf(v)
Ce qu’on peut résumer ainsi : pour toute combinaison linéaire de vecteurs de E (k1v1 + …+ knvn) on a
f(k1v1 + …+ knvn) =
k1f(v1)+ …..+ knf(vn).
En particulier si on écrit
un vecteur dans sa base v = x1b1 + x2b2
+ ….+ xnbn
● On a f(v)= x1
f(b1) + x2 f(b2) + ….. + xn f(bn)
ce qui prouve qu’il suffit de
connaître f(b1), f(b2), …., f(bn)
pour calculer f(v) et connaître f .
Exemples
d’applications linéaires: dans R, f :
x ➜ 3x est linéaire tandis que f : x➜3x + 2 ne l’est pas
Propriétés des applications
linéaires
● f(0E)
= 0F
(il suffit de faire f(0E) = f( v – v) = f(v) – f(v) = 0F
)
● Im ( f ) l’ensemble de toutes les images des éléments
de E par f est un sous espace vectoriel de F
● Ker ( f ) ensemble des vecteurs de E qui on pour image 0F, est un sous espace
vectoriel de E
●
L’ensemble des vecteurs v de E tels que f(v) = kv
(avec k donné) est un sous espace vectoriel de E
● En
particulier c’est le cas des invariants de E qui sont tels que f(v) = v
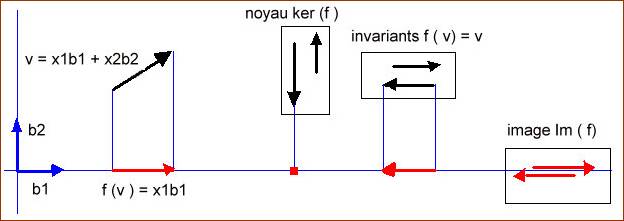
Exemple de la projection du plan de base (b1 ,
b2) sur la droite de base (b1) parallèlement à (b2)
Applications linéaires et matrices
Soit E (base b de dimension n ) et F (base B de dimension p) 2 espaces
vectoriels et f une application linéaire de E dans F . Notre
problème est de trouver les coordonnées de f(v) dans B
quand on connaît les coordonnées de v dans b.
On a vu qu’il suffit de
connaître l’image des vecteurs de la base b f(b1),
f(b2), ., f(bn) pour connaître f
![]() Supposons que f(b1)
= a11B1 + a21B2 + …. + a p1B
p
Supposons que f(b1)
= a11B1 + a21B2 + …. + a p1B
p
. …………………………………… système définissant l’application f
f(bn) = a1nB1 + a2nB2
+ …. + a pn B
p
Si v = x1b1 + x2b2
+ ….+ xnbn
on a f(v) = x1 f(b1) + x2
f(b2) + ….. + xn f(bn) (déf. d’une
appli linéaire)
Si on remplace dans f(v) les f(bi) par leur valeur dans le système 1
on va trouver
En facteur de B1
dans f(v) :
B1 ( x1a11 + x2a12
+ …..+xna1n)
Et en facteur de Bp dans f(v) : Bp
(x1a p1 + x2a p2 + …..+x na
pn)
Donc, les coordonnées de V=f(v) dans la base B en fonction des cordonnées de v dans la
base b :
![]() X1 = x1a11 + x2a12
+ …..+xna 1n
X1 = x1a11 + x2a12
+ …..+xna 1n
………………………………….. Coordonnées de l’image par f de v dans la base B
Xp = x1ap1 + x2ap2
+ …..+xna pn
On symbolise ces calculs de
la manière suivante :

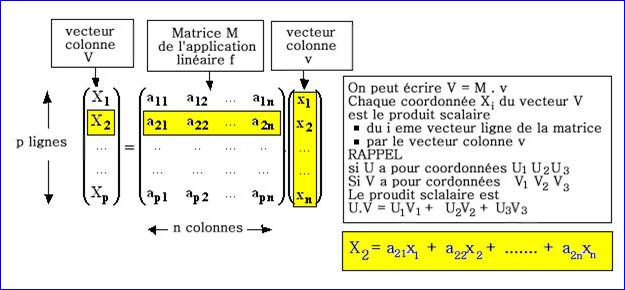
E , base b est un espace vectoriel de dimension n
F , base B est un espace vectoriel de dimension p
f est une application linéaire
de E vers F
À
un vecteur v de E elle fait correspondre un vecteur V de F
La
dimension du vecteur colonne antécédent v
exprimé
dans la base b est celle de E c'est-à-dire n
La
dimension du vecteur colonne image V exprimé dans la base B est celle de F c'est-à-dire p
Les
dimensions de la matrice de f sont n colonnes
X p lignes
Propriétés des matrices liées à une application
linéaire
● si on
rapproche la matrice M d’une application
f de E dans F…
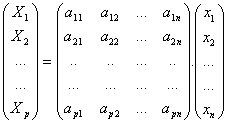
… du système définissant f et donnant l’image des vecteurs de la base b de
E par f
![]() f(b1) = a11B1
+ a21B2 + …. + a p1B
p
f(b1) = a11B1
+ a21B2 + …. + a p1B
p
.
…………………………………… système définissant l’application f
f(bn) = a1nB1 + a2nB2
+ …. + a pn B p
On
observe que les coefficients de la i ème
colonne de la matrice sont les cordonnées de f ( b
i ) dans la base B de F .
Cette
propriété est très utile pour construire
la matrice d’une application linéaire.
Exemple : matrice d’une
rotation d’angle θ dans
le plan ( i , j)
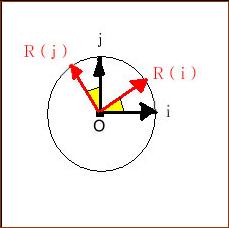 Ici, on est dans un
repère orthonormé (O , i , j) . O est le centre de la
rotation, θ son angle. Il
s’agit d’une transformation ponctuelle.
Ici, on est dans un
repère orthonormé (O , i , j) . O est le centre de la
rotation, θ son angle. Il
s’agit d’une transformation ponctuelle.
La rotation d’un vecteur est assimilée à celle d’un bipoint représentant ce vecteur, le bipoint image représentant le vecteur image.
C’est une application linéaire dans le plan vectoriel rapporté à la base {i , j}
Le centre de rotation perd toute signification dans la rotation vectorielle.
L’image de i est R(i), l’image de j est R(j) .
Les coordonnées de R(i) dans la
base { i, j } sont (cos θ , sin
θ)
Les coordonnées de R(j) dans la base { i, j } sont (–sin θ , cos θ)
Donc dans cette base, la matrice de la rotation
est : ![]()
Exemple : Projection de l’espace {i , j , k} dans
l’espace {i , j} parallèlement à k
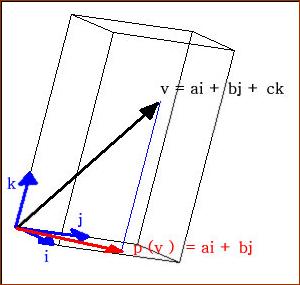 La projection vectorielle p est une application linéaire
La projection vectorielle p est une application linéaire
Le vecteur ai + bj + ck a pour image ai + bj .
L’image de i est i (1 , 0 ) dans la base { i , j }
L’image de j est j (0 , 1 ) dans la base { i , j }
L’image de k est 0 (0 , 0 ) dans la base { i , j }
La matrice de la projection de E rapporté à { i , j , k } dans P rapporté à {i , j} est : ![]()
Im (p ) = plan vectoriel { i , j } Ker (p) = droite vectorielle { k }
Remarques :
● La
composition de 2 applications linéaires f ○ g ,
la somme (f + g ) de 2 applications de E
dans F, le produit par un
scalaire de f (λf) sont des applications
linéaires.
● Dans
tous les cas on a dim (Ker (f ) ) + dim (Im ( f) ) = dim ( E )
● On
appelle rang de f la dimension de Im (f ) .
● Si
une application linéaire f est bijective, on a Ker ( f) = {0E} (Ker (f ) de
dimension 0) et im ( f) = F
donc
rang de f = Dim (E) ou Dim
(F)
● Si une application linéaire est
bijective on a forcément dim (E ) = dim (F) et la matrice de cette application est une matrice
carrée à n lignes et n colonnes.
Mais la réciproque n’est pas vraie .
● Quand une
matrice n’est pas carrée, l’application linéaire qui lui est associée ne peut
pas être bijective. Mais si elle a plus de lignes que de colonnes, elle peut
quelquefois être injective (et donc bijective si on la considère comme une
application de E dans
Im (f)
qui est un sous - espace vectoriel)
● Si
une application linéaire est bijective, elle admet une application linéaire
réciproque f-1 elle aussi associée à une
matrice carrée.
On a f-1○f = f ○
f-1 = IE (identité dans
E )